This program computes the ideal visible fraction or illuminated fraction of the total surface area of a sphere at any distance from the eye or point-light source as reckoned from the center or surface of the sphere.
The radius and distance can be in any convenient linear units. The default values are the mean lunar radius and the mean geocentric lunar distance in statute miles.
In the lunar equations below:
R = Mean Lunar Radius = 1737.05 km = 1079.35 mi
The radius and distance can be in any convenient linear units. The default values are the mean lunar radius and the mean geocentric lunar distance in statute miles.
In the lunar equations below:
R = Mean Lunar Radius = 1737.05 km = 1079.35 mi
For a sphere of radius 1079.35 units, where the distance to the eye or point-light source is 238856 units from the center: Visible or illuminated fraction of surface = 49.774058 percent Invisible or shaded fraction = 50.225942 percent Difference = 0.451884 percent

|
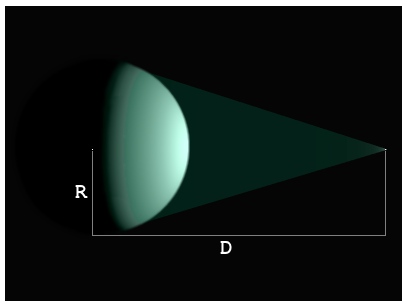
A Sphere and a Point
Mathematically, this is a problem involving a simple point and a sphere in 3D space. The tiny white point in the diagram above could represent different things, depending on the context, for astronomical purposes, the sphere representing a spherical planet or moon.
If the point represented a point-light source, then it would simply illuminate the sphere as shown. The farther away the point, the larger the area reached by the light, but the fainter the recieved light would be, up to a maximum limit of reaching 50 percent of the total surface at infinity. If the point represented the eye or camera lens, then the illuminated area would indicate the ideal fraction of the total spherical surface area visible from that point. The farther away the eye, the greater the visible surface becomes, but the smaller the visible image would be, up to a maximum limit of seeing 50 percent of the total surface at infinity. The distance between the point and the sphere can be reckoned either from the center or from the surface of the sphere, whichever is more convenient or practical for a particular application. The distance between a point and the surface of a sphere equates to the radar distance or the shortest distance between the surface of the sphere and the point. In space, we can send a radar signal to determine our distance from the surface of the moon. This to-the-surface distance is probably more convenient for some applications than using the distance to the center of the moon, such as landing computations. |
 |
|
Where the Distance to the Point is Reckoned
From the Center of the Sphere:
Given the radius ( R) of the sphere and the distance (D) of the point from the center, the general equation for the potential fraction (f) of the total surface area of the sphere as viewed or illuminated from that point is:
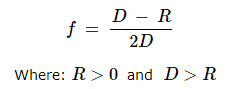 As the distance (
D) from the center of the sphere increases towards infinity, we can see slightly more and more of the surface but then we have to magnify the image more and more to make out details, to the extent of the limits of our imaging technology.
As the distance from the sphere approaches infinity, the potentially visible or illuminated fraction (f) approaches a maximum limit of 0.5 (1/2) of the total surface area.
For the moon, at (D) kilometers or statute miles from the center: 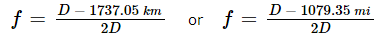 |
 |
|
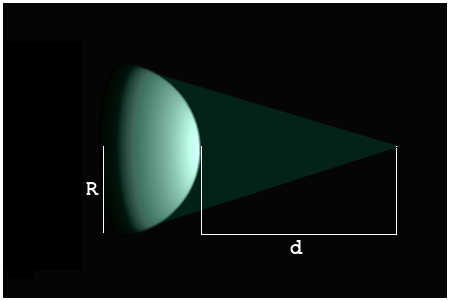
Where the Distance to the Point is Reckoned
From the Surface of the Sphere:
Given the radius (R) of the sphere and the distance (d) of the point from its surface, the general equation for the ideal fraction (f) of the total surface area of the sphere as viewed or illuminated from that point is:
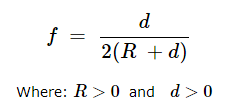 As the distance from the surface of the sphere approaches infinity, the potentially visible or illuminated fraction (f) approaches a maximum limit of 0.5 (1/2) of the total surface area.
For the moon, at (d) kilometers or statute miles from the surface:
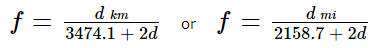 In the lunar equations above: R = Mean Lunar Radius = 1737.05 km = 1079.35 mi 2026 - Jay Tanner
|